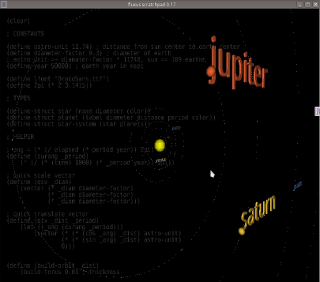
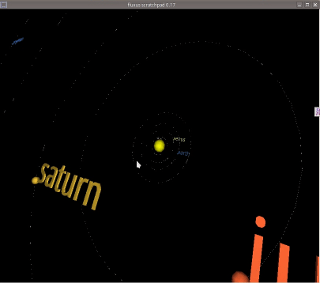
Some time ago I wrote a post about fluxus, livecoding and 3D-prototyping system. Now I want to demonstrate some of its features and describe how you may use them in pseudo(;))scientific needs. For example, you can create a model of a simplified solar system and make it fit in only 125 lines of code (including comments) – it is the advantage of Racket language with graphic steroids, the core of fluxus and a descendant of PLT Scheme. Here how the result will look like:
There are sources in the post, a short desription of code structure, tutorial movies in Slavic English, examining in detail the whole process of writing this complicated (;)) code.
Sources
Note: Since it was lost with the Poocoo, I’ll try to restore it from video.
Description
Fluxus uses a term of state machine for scene construction. If you have programmed in OpenGL already, you are familiar with this principle - every next function in the code either modifies the matrix of scene state or changes the content of the scene (i.e. draws an object). You may construct the required scene objects just before any rendering will happen and then change their conditions later or just draw a new primitives in every frame (OpenGL understands that it may cache the objects which state is not changed a lot between frames). I am using the both ways of these, so I prepare the text labels and planets' orbits before rendering process but I draw planets in every new frame.
I have taken all the data about equatorial diameters, orbital radiuses and orbital periods of the planets from the single one table in Wikipedia article. It is very handy that all parameters are presented relatively to Earth properties (that is how astronomical units are calculated), so the Earth diameter and Earth year can be used as system of units in our model.
Do you know that distance from mass center of Earth to mass center of Sun is approximately equal to 11740 Earth diameters? It is the astronomical unit (
astro-unitconstant) and the distances from Sun to planets are measured relativey to it. And more, 109 Earth diameters fits the diameter of Sun (the Earth diameter is represented withdiameter-factorconstant in the model).
When we know this data, we can calculate the angles for planets positions (the orbital eccentricities are not taken in account in the model, it’s a homework) and place them appropriately in the model.
Examining code
star,planetand planetary system (it is calledstar-systembecause the center of it is a star), consisting of star and planets, structures are defined- defined functions of
- getting translate vector (
qtv- quick translate vector) for planet using its orbital radius and orbital period - getting scale vector (
qsv- quick scale vector) of planet using its diameter - fast calculation of planet position angle (
curang), relatively to (Sun) (0, 0) point, using planet’s orbital period - building orbit primitive (
build-orbit) using its orbital radius - building label primitive (
qto- _quick text object`) for planet using the passed string
- getting translate vector (
- the star of Sun is created, planets and all of them are put into “solar system” instance (
solar-system). while filling planets structures, the labels primitives are built for each one. - using the planets data the orbits are built
- functions are defined
draw-star, it draws a stardraw-planet, it draws a planet in the required position depending on current time and moving the text label in the same position
renderfunction is defined, it draws sun and planets one by one, callingdraw-staranddraw-planetrenderis assigned to be a function executed for each frame
Videos
Fluxus Livecoding: Building 3D Solar System / Part 1 from Ulric Wilfred on Vimeo.
Fluxus Livecoding: Building 3D Solar System / Part 2 from Ulric Wilfred on Vimeo.
Fluxus Livecoding: Building 3D Solar System / Part 3 from Ulric Wilfred on Vimeo.